Brahmagupta Calculator

About Brahmagupta

Brahmagupta, an ancient Indian mathematician and astronomer who lived in the 7th century, made significant contributions to mathematics, particularly in the fields of algebra and geometry. One of his notable works is the “Brahmasphutasiddhanta,” which covers various mathematical concepts, including arithmetic, algebra, and trigonometry.

Brahmagupta’s Contributions to Calculation:

• Arithmetic Operations:
  • Brahmagupta provided rules for arithmetic operations, including addition, subtraction, multiplication, and division. He also worked with fractions and negative numbers.
• Zero and Negative Numbers:
  • Brahmagupta was one of the first mathematicians to formally define zero and its properties. He also established rules for dealing with negative numbers, such as:
    • The product of two negative numbers is positive.
    • The product of a positive and a negative number is negative.
• Quadratic Equations:
  • Brahmagupta gave methods for solving quadratic equations of the form ax2+bx=cax2+bx=c. His approach was similar to the modern quadratic formula.
• Brahmagupta’s Formula:
  • In geometry, Brahmagupta is known for his formula to calculate the area of a cyclic quadrilateral (a four-sided figure where all vertices lie on a circle). The formula is:
  • Area=(s−a)(s−b)(s−c)(s−d)​
• Interpolation:
  • Brahmagupta developed methods for interpolation, which were used in astronomy to estimate values between known data points.
• Trigonometry:
  • He contributed to early trigonometry by providing tables of sine values and formulas for trigonometric identities.

The Brahmagupta Formula is a mathematical formula used to calculate the area of a cyclic quadrilateral (a four-sided polygon where all vertices lie on a single circle). It is named after the ancient Indian mathematician Brahmagupta, who introduced it in the 7th century.

The Formula:

For a cyclic quadrilateral with side lengths a,b,c and d, the area A is given by:

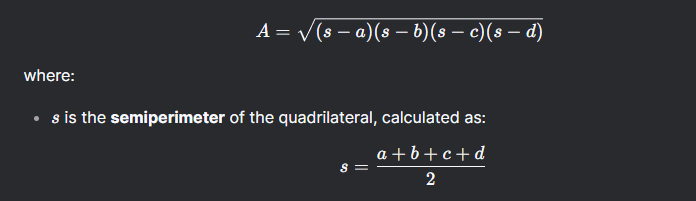
Key Points:

• Cyclic Quadrilateral:
  • The formula only works for quadrilaterals that can be inscribed in a circle (i.e., all four vertices lie on a circle).
• Similarity to Heron’s Formula:
  • Brahmagupta’s formula is an extension of Heron’s formula, which calculates the area of a triangle. Heron’s formula is:

where s is the semiperimeter of the triangle.

• Special Case: Triangle:
  • If one side of the cyclic quadrilateral becomes zero (e.g., d=0d=0), the formula reduces to Heron’s formula for a triangle.
• Non-Cyclic Quadrilaterals:
  • The formula does not apply to quadrilaterals that are not cyclic. For general quadrilaterals, other methods (like Bretschneider’s formula) must be used.

Example:

Consider a cyclic quadrilateral with side lengths a=5a=5, b=6b=6, c=7c=7, and d=8d=8.

1. Calculate the semiperimeter s: